Crypto
Chaos
在此之前有必要先说一下数字签名是什么:
偷个懒,并且我的口语表述一定不如AI。
1. 生活中的签名 vs 数字签名
-
生活中的签名
当你签合同、写一张支票时,你要在上面签上你的名字 ✍️。- 证明:是你本人签的(别人伪造会很难)。
- 保证:签完之后内容不被随意篡改,否则签名就“不对应了”。
-
数字签名
在计算机世界里,我们经常需要验证:- 这条消息/文件,确实是某个人/服务器发出来的,而不是伪造的。
- 收到的消息,在传输过程中没有被篡改。
👉 于是“数字签名”就诞生了:用数学方法,替代你在合同上写字的作用。
2. 签名的三个主要用途
-
身份认证
- 只有拥有私钥的人,才能生成正确签名。
- 比如:消息带着合法数字签名,就能确定它来自 Alice,而不是冒充者。
-
数据完整性
- 如果消息在传输中哪怕改了一个字母,签名验证就通不过。
- 所以签名能保证“没人动过里面的内容”。
-
不可否认性
- 因为签名只能由私钥的持有者生成,事后不能抵赖。
- 就像你签合同:签了就不能说“不是我签的”。
3. 在网络安全/CTF中的应用
-
HTTPS / SSH / GPG 这些协议里,都用到了数字签名来保证身份和完整性。
-
在 CTF 中,签名算法常常被作为考点。出题人会特意设置:
- 用弱随机数生成签名(导致私钥可被破解);
- 或者暴露部分签名流量,让选手尝试恢复私钥。
4. 一个小小的类比 🔒
假设:
- 你有一个“秘密图章”,世界上只有你一个人有(这就是私钥)。
- 你在一份文件上盖章(数学运算 → 生成签名)。
- 任何人拿到盖过章的文件,都能去“政府机关”(公钥)验证章是真的还是假的。
这样就能保障:
- 任何人都可以验证来源真伪;
- 但只有你能“盖章”。
这就是数字签名的用武之地。
✅ 总结
数字签名的 作用 就是:
👉 证明消息是谁发的 + 确认消息没有被篡改 + 防抵赖
在你的 CTF 题里,服务器就好比是“政府机关”,它不会相信你发的 "give_me_flag",除非你附带的 (r,s) 签名是 匹配你私钥的盖章。
🔑 一、DSA的基本设定
DSA(Digital Signature Algorithm)基于有限域的 离散对数问题。
简单来说,离散对数问题就是:
给定 y=g^x(mod p),知道 g 和 y 之后,想求 x 是非常难的。
这就像:
- 乘法很容易算:2^7=128
- 但反过来问:2^x=128,求 x?在模大素数下就非常难!
- 这种“单向难题” 就是 DSA 的安全基础。
⚙️ 二、参数 & 密钥
- 选取大素数 p 和素数 q∣(p−1)。
- 找到生成元 g=h^(p−1)/q。
- 私钥 x∈[1,q−1]。
- 公钥:y=g^x(modp)。
其中:
- p:一个大素数(常见是 512 位或者 1024 位)。
这里的位是二进制位数,也就是2^1024 约为十进制1.8*10 ^308 - q:一个较小的素数,通常 160位。
- "∣":整除符号,a∣b 表示 a 可以把 b 整除没有余数。
所以:
q∣(p−1)⟺(p−1)modq=0.
👉 所以系统的密钥对是:
- 公钥:(p,q,g,y)
- 私钥:x
🖊️ 三、签名原理
签名过程要对消息 m 输出一个签名 (r,s)。
公式:
- 对消息哈希(H(m)是消息的哈希值):
h=H(m) (mod q) - 生成随机数(一次性 nonce,必须保证安全):
k∈{1,2,…,q−1} - 计算:
r=(g^k mod p)mod q - 计算:
s=k^(−1) * (h+x⋅r) (modq) - 输出签名 (r,s)。
🔍 四、验证原理
验证者有消息 m,签名 (r,s),公钥 (p,q,g,y):
- 检查 0<r,s<q。
- 计算 h=H(m)(modq)。
- 计算:w=s−1(modq)u1=h⋅w(modq)u2=r⋅w(modq)
- 计算:v=(gu1⋅yu2modp)modq
- 若 v=r,签名有效。
🧮 五、为什么验证能成功?
重点在于用代数演算,证明 签名生成的 r 在验证时能还原出来。
签名时:
s≡k−1(h+xr)(modq)所以:
w=s−1≡h+xrk(modq)于是:
u1=h⋅w≡h+xrhku2=r⋅w≡h+xrxrk验证要求计算:
v=(gu1⋅yu2modp)modq代入 y=gx:
v≡gu1⋅(gx)u2≡gu1+xu2(modp)再代入 u1,u2:
u1+xu2=h+xrhk+h+xrxrk=h+xr(h+xr)k=k所以:
v≡gk(modp)≡r(modq)👉 完全吻合!这证明了为什么合法签名在验证时成立。 🎉
📖 六、关键点
- 为什么要每次都换 k?
因为如果复用了同一个 k,攻击者可以通过两条签名方程直接消元,恢复私钥 x。
如果 k 可预测(伪随机数),也可以恢复 x。 - 安全性来自离散对数问题:
不知道 x 的情况下,几乎不可能反推签名,除非随机数 k 泄露。
✅ 总结
DSA的原理:
- 建立在 离散对数难题 上(y=gx(modp))。
- 签名 = 用私钥 x 和随机数 k 混合生成 (r,s)。
- 验证 = 公钥替代私钥,重新推导出 r,看是否匹配。
- 数学保证成立,除非有人能解离散对数。
⚡ 这就是 DSA 的全流程与原理!
params.txt:
p = 8576266215257684451627938266209288368747290850430257232775662794860889167273173590976498454387838065099555150702527005228232224203671818388040396426167421
q = 1092510234019
g = 7144062426562178459134763982605952302933077316845461785177531950627385795442407387260745982564084210402482982761274236868248912040071369181916889827118820
x = 379478523492
y = 8291891676739439066670566927114794141859628227389282017383200710395666779939972786268373568231932748094932532880440197180527838969047845790921891292250679
P_bits= 512
NUM_SAMPLES:= 700
观察server.py
class Handler(socketserver.BaseRequestHandler):
def handle(self):
self.request.sendall(b"Send me JSON lines like {\"msg\":\"...\",\"r\":\"...\",\"s\":\"...\"}\n")
while True:
line = self.request.recv(4096).strip()
if not line:
break
try:
data = json.loads(line.decode())
msg = data['msg']
r = int(data['r'])
s = int(data['s'])
ok = verify(msg, r, s)
self.request.sendall(f"MSG={msg} OK={ok}\n".encode())
if ok and msg == "give_me_flag":
self.request.sendall(f"FLAG: {FLAG}\n".encode())
break
except Exception as e:
self.request.sendall(f"Error: {e}\n".encode())
我们只需要伪造签名,在json里面传入give_me_flag 以及签名即可
#!/usr/bin/env python3
import socket
import json
from hashlib import sha1
# --- Public parameters (题目给的) ---
p = 8576266215257684451627938266209288368747290850430257232775662794860889167273173590976498454387838065099555150702527005228232224203671818388040396426167421
q = 1092510234019
g = 7144062426562178459134763982605952302933077316845461785177531950627385795442407387260745982564084210402482982761274236868248912040071369181916889827118820
# 已知私钥
x = 379478523492
# --------- 工具函数 ----------
def modinv(a, m):
"""模逆 (扩展欧几里得算法)"""
a = a % m
lm, hm = 1, 0
low, high = a % m, m
while low > 1:
r = high // low
nm, new = hm - lm * r, high - low * r
lm, low, hm, high = nm, new, lm, low
return lm % m
def sign(msg: str, x: int):
"""使用 DSA 签名公式生成 (r, s)"""
k = 13371337 # 任意选一个 k,保证 gcd(k,q)=1
r = pow(g, k, p) % q
hm = int.from_bytes(sha1(msg.encode()).digest(), 'big') % q
s = (modinv(k, q) * (hm + x * r)) % q
return r, s
# --------- EXPLOIT ----------
def main():
msg = "give_me_flag"
r, s = sign(msg, x)
payload = {
"msg": msg,
"r": str(r),
"s": str(s)
}
with socket.create_connection(("101.37.152.107", 40356)) as sck:
# 读取欢迎信息
print(sck.recv(4096).decode())
# 发送 JSON 数据
sck.sendall((json.dumps(payload) + "\n").encode())
# 打印返回
while True:
data = sck.recv(4096)
if not data:
break
print(data.decode(), end="")
if __name__ == "__main__":
main()
RSA_Shrimp
本题为弱私钥攻击。首先来理解一下RSA加密的原理
1.随机生成了两个较大的质数p q
2.N=p*q
3.f(N) = (p-1)(q-1)
4.选择公钥指数e 私钥指数d 要 e⋅d≡1(modφ(N))
(简单来说 就是e * d 的结果除上步骤三函数的值会余下1 就是 e⋅d=k⋅φ(N)+1)
这里的e是选择出来的,要求和f()的计算结果互质。 而d是根据公式自行计算出来的
加密:
c=m^e(modN)
解密:
m=c^d(modN)
这里 m 就是message 要先变成数字才可以传入RSA公式
c就是 ciphertext 也就是密文 是经过加密公式得到的结果
那么来看这道题,结合上面的解析。逐行注释
from Crypto.Util.number import *
flag = b"*************************" #加密字符串
m = bytes_to_long(flag) #转换成字节长度
p = getPrime(512) #获取一个512位的质数
q = getPrime(512) #获取一个512位的质数
N = p * q #计算N
phi = (p-1) * (q-1) #计算刚才提到的函数f(N)
while True: #这里起了一个循坏在爆破 通过较小的d猜测
d = getRandomNBitInteger(100) #生成一个100bit长度的整数 差不多是30位十进制
if GCD(d, phi) == 1: #检查是否互质 最大公约数=1
e = inverse(d, phi) #如果是 就去计算e
break
c = pow(m, e, N) #这里在计算加密结果了
print("N =", N)
print("e =", e)
print("c =", c)
# N = 68746286008550900561211884501893911659857156943721084790337122697824152725388556385094324431207100918046967638587952452006699674073267880815284571377923522568540860578928958047237963906801078412732075997418412620971167170469734625762375930514876132441068524255367879916677634221816923228079121571548347850289
# e = 24006058401963947504489286096623012205003559131381699235161658259462698881635631685205499256684381203102886817004913000773423816418776591869027514152368812643891357226415333262897367798329023818025568613986801911330633284000994070975248246673005349619151136178874159238632086935536449090286571988916222816845
# c = 23720964276942320591253561961648374040271688288569750833058337665367095773075582380308232092705492932255383791571090487445664544611052993739592283813442185798551807147870302766040670104074525384923333796562348827180648346095823791921772906857810787862771014225519300879806146412190941439992602318514593025722
最后的注释 已经告诉了我们 N e c的具体数值,根据前面学习的的知识以及对加密程序的分析 我们知道了:
要知道m 需要计算 m=c^d(modN) 目前我们已经知道了N c 但是d还不知道。
d是通过100bit随机生成出来的 并且满足 d=(k⋅φ(N)+1)/e 并且我们已经知道了e
可目前我们最大的问题 就是在于不知道φ(N)的值是多少。
在这里引入一个新的概念:维纳攻击 wiener attack

下一步我们要做的 就是编写相关的python程序 直接爆破
from Crypto.Util.number import long_to_bytes
import math
# -------------------------
# 连分数展开
# -------------------------
def continued_fraction(n, d):
while d:
q = n // d
yield q
n, d = d, n - q * d
def convergents(cf):
convs = []
for i in range(len(cf)):
num, den = 1, 0
for j in reversed(cf[:i+1]):
num, den = den + j*num, num
convs.append((num, den))
return convs
def wiener_attack(e, N):
cf = list(continued_fraction(e, N))
for k, d in convergents(cf):
if k == 0:
continue
if (e*d - 1) % k == 0:
phi = (e*d - 1)//k
# 解二次方程 x^2 - (N - phi + 1)x + N = 0
a = 1
b = -(N - phi + 1)
c = N
disc = b*b - 4*a*c
if disc >= 0:
sqrt_disc = math.isqrt(disc) # 整数开方
if sqrt_disc*sqrt_disc == disc:
return d
return None
# -------------------------
# 题目给的参数
# -------------------------
N = 68746286008550900561211884501893911659857156943721084790337122697824152725388556385094324431207100918046967638587952452006699674073267880815284571377923522568540860578928958047237963906801078412732075997418412620971167170469734625762375930514876132441068524255367879916677634221816923228079121571548347850289
e = 24006058401963947504489286096623012205003559131381699235161658259462698881635631685205499256684381203102886817004913000773423816418776591869027514152368812643891357226415333262897367798329023818025568613986801911330633284000994070975248246673005349619151136178874159238632086935536449090286571988916222816845
c = 23720964276942320591253561961648374040271688288569750833058337665367095773075582380308232092705492932255383791571090487445664544611052993739592283813442185798551807147870302766040670104074525384923333796562348827180648346095823791921772906857810787862771014225519300879806146412190941439992602318514593025722
# -------------------------
# 攻击过程
# -------------------------
print("[*] 运行 Wiener Attack...")
d = wiener_attack(e, N)
if d:
print("[+] 成功找到 d =", d)
m = pow(c, d, N)
print("[+] 明文 =", long_to_bytes(m))
else:
print("[!] 攻击失败")
得到运行结果:

Wilderness
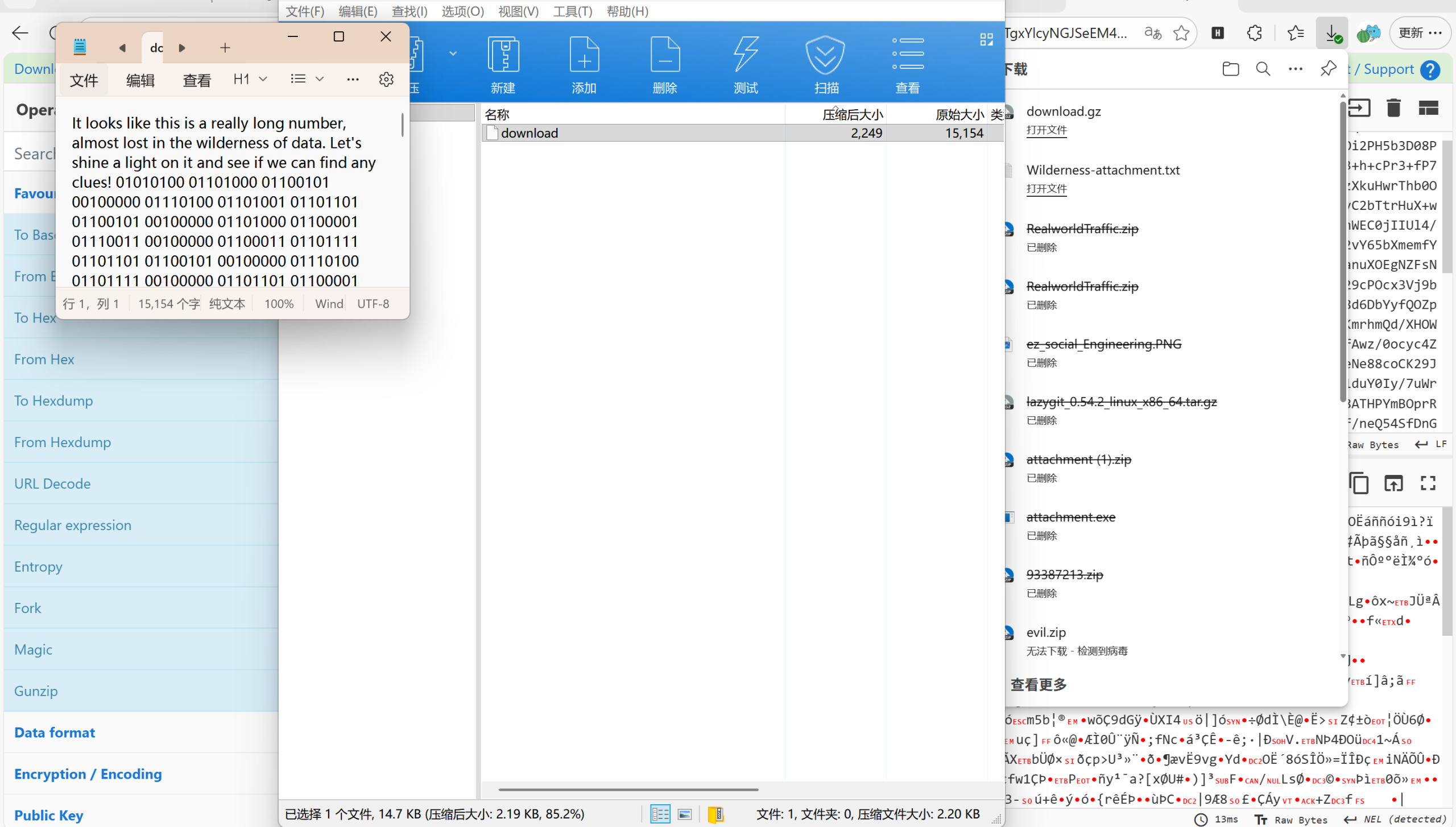
cyberchef解码得到一个新的文件
binary_str = """
01010100 01101000 01100101 00100000 01110100 01101001 01101101 01100101 00100000 01101000 01100001 01110011 00100000 01100011 01101111 01101101 01100101 00100000 01110100 01101111 00100000 01101101 01100001 01101011 01100101 00100000 01100001 00100000 01100011 01101000 01101111 01101001 01100011 01100101 00101110 00100000 01000011 01101000 01101111 01101111 01110011 01100101 00100000 01110111 01101001 01110011 01100101 01101100 01111001 00101100 00100000 01101111 01110010 00100000 01111001 01101111 01110101 00100000 01110010 01101001 01110011 01101011 00100000 01101100 01100101 01110100 01110100 01101001 01101110 01100111 00100000 01111001 01101111 01110101 01110010 00100000 01101000 01100101 01100001 01110010 01110100 00100000 01100010 01100101 01100011 01101111 01101101 01100101 00100000 01100001 00100000 01101110 01100101 01110111 01100101 01110010 00100000 01110111 01101001 01101100 01100100 01100101 01110010 01101110 01100101 01110011 01110011 00101100 00100000 01100001 01101110 01100100 00100000 01110100 01101000 01100101 00100000 01110100 01110010 01110101 01100101 00100000 01100110 01101100 01100001 01100111 00100000 01101101 01100001 01111001 00100000 01110010 01100101 01101101 01100001 01101001 01101110 00100000 01101000 01101001 01100100 01100100 01100101 01101110 00100000 01101001 01101110 00100000 01110100 01101000 01100101 00100000 01110011 01101000 01100001 01100100 01100101 00101110
"""
bytes_list = [int(b, 2) for b in binary_str.split()]
text = ''.join(chr(b) for b in bytes_list)
print(text)
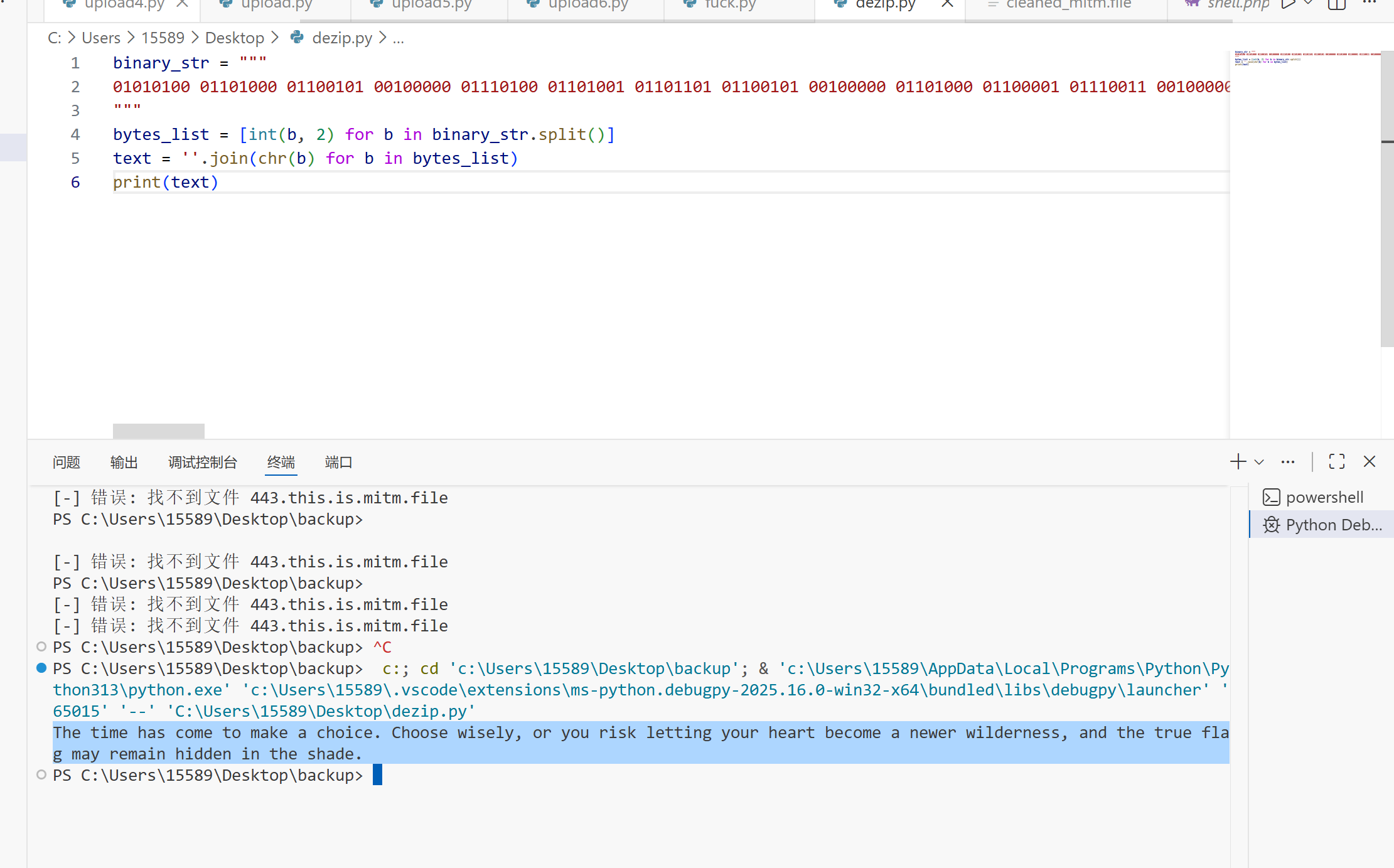
The time has come to make a choice. Choose wisely, or you risk letting your heart become a newer wilderness, and the true flag may remain hidden in the shade.
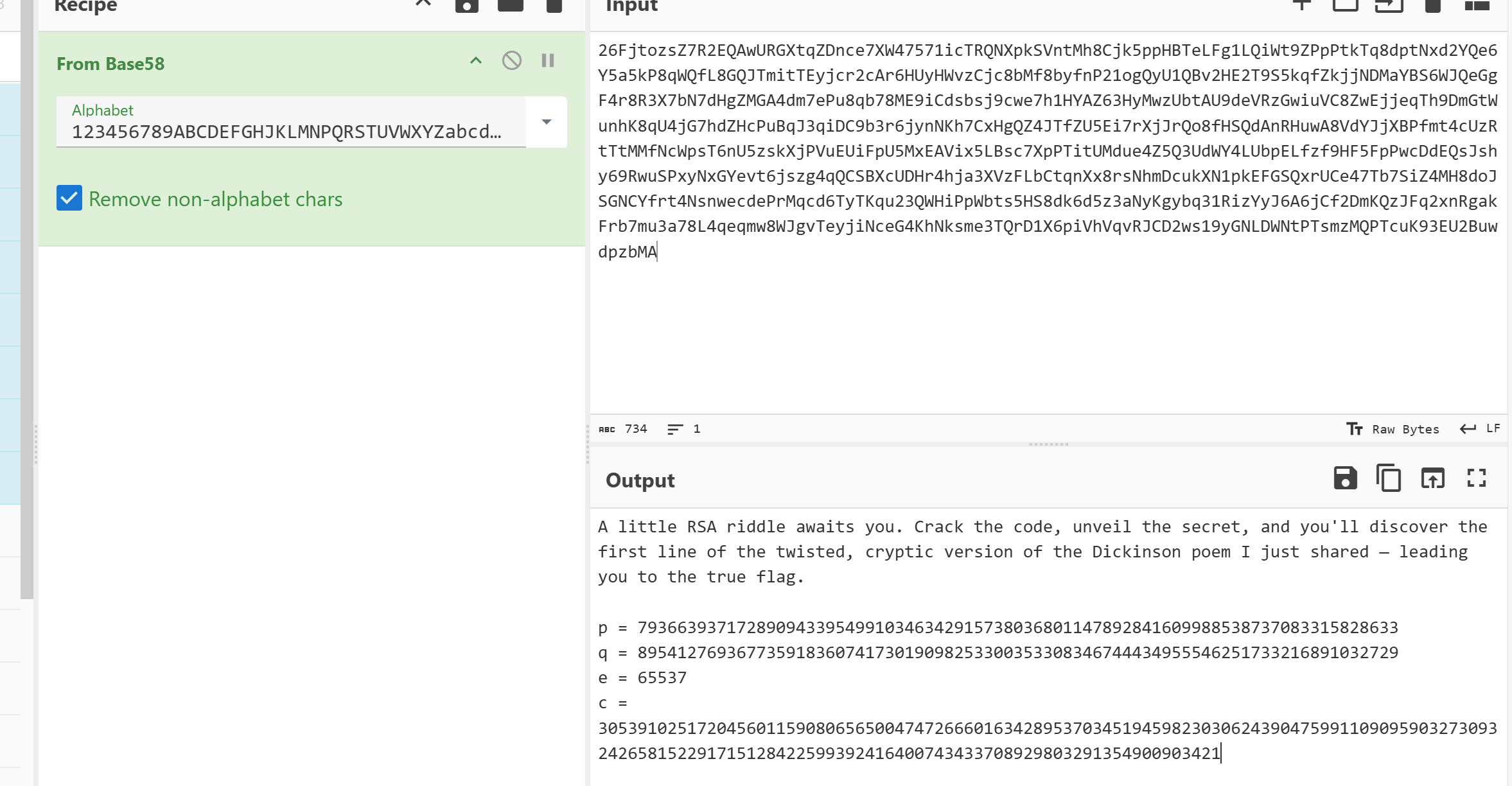
p = 79366393717289094339549910346342915738036801147892841609988538737083315828633
q = 89541276936773591836074173019098253300353308346744434955546251733216891032729
e = 65537
c = 3053910251720456011590806565004747266601634289537034519459823030624390475991109095903273093242658152291715128422599392416400743433708929803291354900903421
# 1. 计算 n
n = p * q
# 2. 计算 φ(n)
phi = (p - 1) * (q - 1)
# 3. 计算 d = e^(-1) mod φ(n)
d = pow(e, -1, phi) # Python 3.8+ 支持
# 4. 解密:m = c^d mod n
m = pow(c, d, n)
print("m (int) =", m)
# 5. 转成字节再看文本
# 把整数 m 转成足够长度的 bytes(去掉最高位的 0)
m_hex = format(m, "x") # 先转 hex 字符串
if len(m_hex) % 2: # 若长度是奇数,补一个前导 0
m_hex = '0' + m_hex
m_bytes = bytes.fromhex(m_hex)
try:
text = m_bytes.decode('utf-8', errors='ignore')
print("m (as text) =")
print(text)
except Exception as ex:
print("decode error:", ex)
print("raw bytes:", m_bytes)
